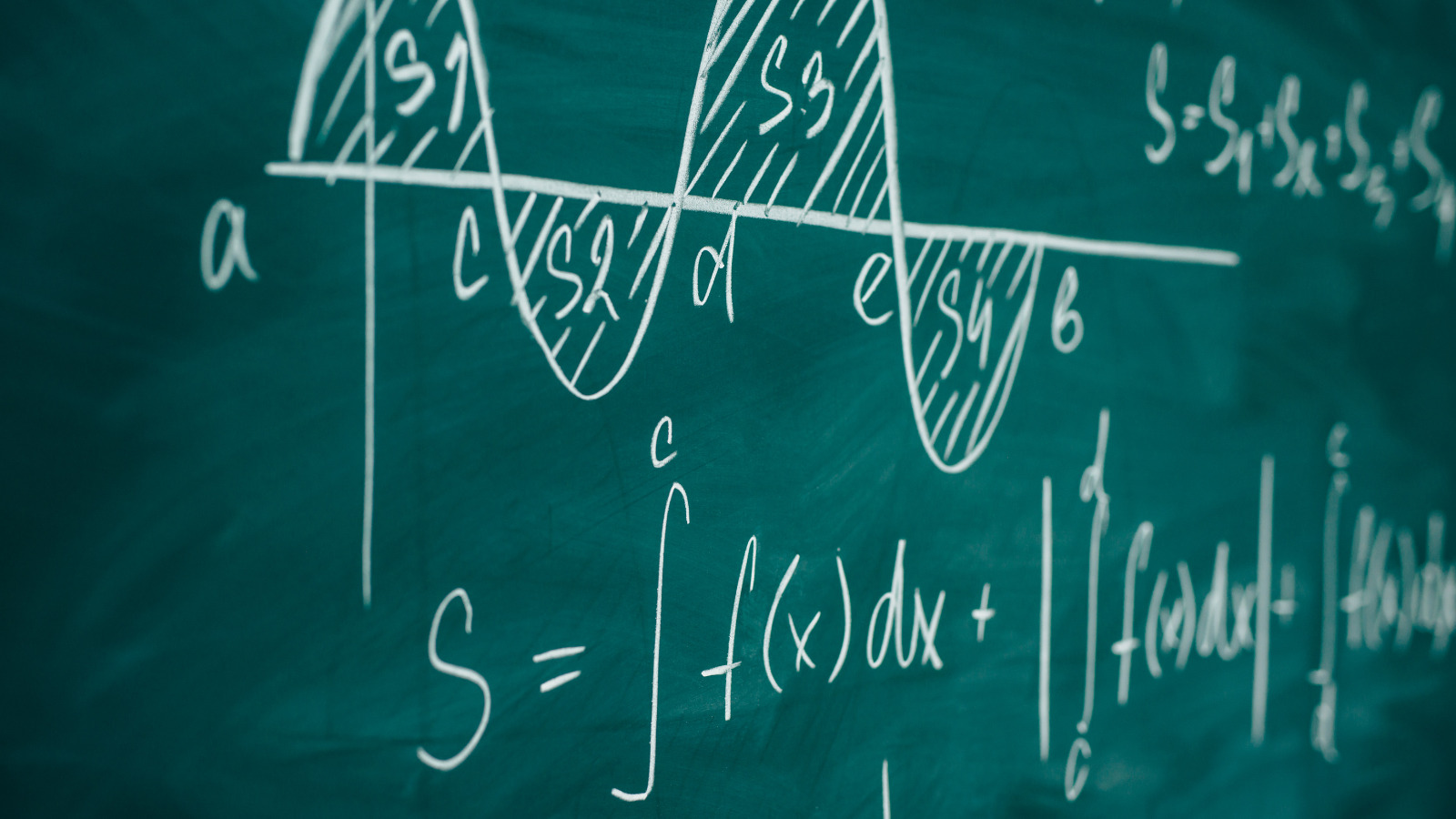微分積分の意味がわからない！何に使うのかわかりやすく解説

「微分積分の意味がわからない！」そんなお悩みにお応えして、「微分積分は何に使うのか」「イメージ」などをわかりやすく解説します。

＼　今すぐチェック！　／

微分積分の意味がわからない人は多い

高校数学で勉強をする「微分」「積分」ですが、計算自体がとんでもなく難しいというわけではありません。

しかし、そもそも一体なんのための計算をやらされているのか、

「微分積分って何？」「微分積分の意味がわからない……」

と思っている人は多いはず。

元教師の私も、高校時代には「何やってるんだろう……」と微分積分の分野に関してはモヤモヤしたまま過ごしていました。

正直、微分積分の意味がわからない人は多いと感じています。

微分積分が難しい理由は？

なぜ微分積分が難しいと言われているのか。

その理由は4つあります。

よくわからない文字がたくさん出てくる

微分積分が難しいと感じる理由の1つは「よくわからない文字がたくさん出てくる」から。

微分積分を勉強していると、「lim」や「Δx」「f'(x)」といった文字が出てきます。

数学が苦手な人は、こういった「文字アレルギー」である可能性が高いです。

問題に文字がたくさん出てくるだけで頭がパニックになり、やる気もなくなってしまうという人も多いようですよ。

こういった文字に慣れるには、とにかく計算問題をたくさんこなすことです。

より多くの計算問題を解くと、文字に見慣れますし、意味もだんだんわかってきます。

中学数学との違いがわからない

微分積分を突然理解しようとしても難しいです。

数学を勉強する上で大切なのは、これまで学習してきた内容との関連性を考えること。

後ほど、「中学数学で習ったことと微分積分の違い」や「微分積分を計算するメリット」をご紹介します。

イメージがわかない

微分積分を勉強する上で、イメージが湧かないという人も多いでしょう。

微分や積分を勉強する前に、ざっくりでも良いのでイメージが持てると好スタートをきれます。

後ほどイメージについて解説します。

実生活に役立つ気がしない

数学が嫌いになる原因は、「何のために勉強するのかわからない」というモヤモヤした感情です。

実際、微分積分の基本的な計算は決して難しいわけではありません。

しかし、何のためにやっているのか、実生活に役立つイメージが湧かないため、やる気が起こらず、理解も浅くなってしまっているのだと思われます。

後ほど実生活のどの部分で使われているのか、微分積分が役立っているシーンをご紹介します。

微分積分のイメージをわかりやすく解説

「微分積分」という言葉や「lim」「∫」などの文字とにらめっこしていても始まりません。

まずは、ザックリとしたイメージで理解してみましょう。

微分は「細かくわけて考えること」

微分は、「細かくわけて考える」ことです。

『微分』という言葉自体のそれぞれの意味をとってみると

となり、なんとなく理解できそうです。

微分はいわば、微小な変化を考える作業なのです。

ただし、単純な微分の計算で求められる生活に直結するような良い具体例がないため、ちょっとわかりやすくくなっています。

高校の学習範囲では「曲線における接線の傾き（曲線の曲がり具合）」や「瞬間の速さ」を求めることになります。

全体像ではなく、「ある一点」「一瞬」における変化量を求めるわけです。

「微分って何？」と思ったら、とりあえず「細かくわけて考えること」だとイメージを持っておきましょう。

詳しい計算はまた後で解説します。

積分は「細かくわけたものを集めて考えること」

一方で積分は、「細かくわけたものを集めて考えること」です。

『積分』という言葉自体のそれぞれの意味をとってみると

となり、なんとなく理解できそうです。

高校数学では、曲線で囲まれた図形の面積を求めることが多いですね。

そのため、微分よりも積分の方がイメージしやすいと思います。

「積分って何？」と思ったら、とりあえず「細かくわけたものを集めて考えること」だとイメージを持っておきましょう。

中学数学ではなかった！微分積分を勉強するとできるようになること

微分積分とはズバリ、「細かく分けてみたり、それを集めて分析することで未来を予測する」ための道具です。

実生活では、株価の推移や渋滞予測などに使われます。

しかしそれ以前に、「微分」や「積分」を学習することで何ができるようになるのでしょうか。

中学校までに習った学習と比較しながら「微分積分を習うとできるようになること」を解説していきます。

微分を勉強する意味

高校数学における微分の役割は「曲線の傾き具合いを計算する」ことにあります。

微分は
曲線のグラフを正確に書くための道具

中学校までの学習では、1次関数の傾きを勉強してきました。

それに対し、2次関数の傾きは一定ではありません。

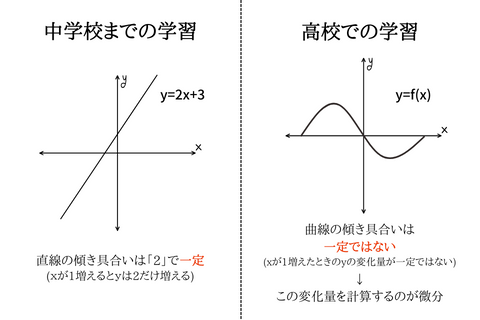
曲線の傾き具合は、場所によってことなります。

この一定ではない値を計算するのが微分なのです。

積分を勉強する意味

高校数学における積分の役割は「”曲線”で囲まれた面積を求めること」にあります。

積分を使うことで「直線」だけでなく
「曲線」で囲まれた図形の
面積が求められるようになる！

中学校までの学習では、長方形や三角形など、直線で囲まれた図形の面積や円の面積を求めてきました。

中学までに習う図形の面積

図形	面積の求め方
三角形	(底辺)×(高さ)÷2
長方形	(縦)×(横)
台形	(上底+下底)×(高さ)÷2
ひし形	(対角線)×(対角線)÷2
平行四辺形	(底辺)×(高さ)
円	(半径)×(半径)×3.14

これらは直線で囲まれたりと、単純な図形の面積です。

しかし、高校ではもっと難しい面積も求められるようになるのです。

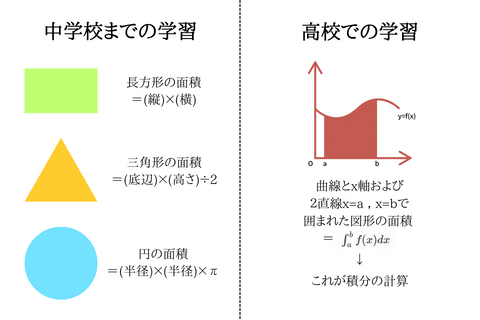
積分を使うことで、直線で囲まれた面積ではなく曲線で囲まれた図形の面積を求めることができるようになります。

$曲線とx軸および2直線x=a,x=bで$
$囲まれた図形の面積$
$=\int_{a}^{b}f(x)dx$

微分積分は何に使う？実生活で役立つ例を紹介

微分積分の計算なんて生きてて使ったことがないよ……という人も多いでしょう。

正直に言うと、私も数学の授業以外で微分積分の計算をしたことはありません。

しかし、微分積分は世の中のあらゆるものに貢献しています。

コンピュータが微分積分を用いた計算を行なってさまざまな予測をたてることで、私たちの暮らしはより豊かなものになっているのです。

実際には、以下のような場面で微分積分が使われています。

どれも複雑な数式が使われており、単純な微分積分の計算ではありません。

例えば、足し算や引き算はお金の計算に必要とされるため、「買い物で役立つ」という実感があると思います。

しかし、微分積分の計算方法を勉強したとしても、それが直接的に必要となる場面が限られています。

そのため、微分積分が役立つという実感が湧かないかもしれません。

しかし、実際には微分積分はあらゆる分野で活用されており、私たちの暮らしに役立っていることは確実です。

社会に出て微分積分の計算をすることはないかもしれませんが、その本質を理解することは長い人生の中で決して無駄にはならないでしょう。

「微分積分の意味がわからない！」という人は、問題を解くよりもまずは関連マンガ・本を読むのもありです。

以下の記事でおすすめを紹介していますので、良かったら参考にしてみてくださいね。