高校数学の「場合の数と確率」でPとCを習うと、どっちを使えば良いのかわけがわからなくなることってありませんか。
そこで今回は、確率の計算で出てくる「P」と「C」と「!(階乗)」の使い分けをわかりやすく解説していきます。
\ 今すぐチェック! /
のキャンペーン
確率の計算「PとCと!」の違い


そもそも計算の前に、確率で出てくるPとCと!の意味をまず頭に入れておきましょう。
!(階乗)の定義と具体的な計算方法
いわゆる「ビックリマーク」は「かいじょう」と読みます。
この記号が出てきたら、1から「!」の前に書かれた数までのすべての数を掛けます。
$$n!=n(n-1)(n-2)・・・1$$
具体的な計算方法は、以下の通りです。
$$6!=6×5×4×3×2×1=720$$
Pの定義と具体的な計算方法
Pは「permutation」の頭文字です。
順列の計算で出てきます。
$${_nP_r}=\dfrac{n!}{(n-r)!}$$
具体的な計算方法は、以下の通りです。
$${_6P_4}=\dfrac{6!}{(6-4)!}=360$$
Cの定義と具体的な計算方法
Cは「combination」の頭文字です。
組み合わせの計算で出てきます。
$${_nC_r}=\dfrac{n!}{r!(n-r)!}$$
具体的な計算方法は、以下の通りです。
$${_6C_4}=\dfrac{6!}{4!(6-4)!}=15$$
ただし、有名な性質として以下の計算方法がよく用いられることを覚えておきましょう。
$${_nC_r}={_nC_{n-r}}$$ただし$$0≦r≦n$$
具体的な計算方法は、以下の通りです。
$${_6C_4}={_6C_{6-4}}={_6C_2}=\dfrac{6!}{2!(6-2)!}=15$$
この3つの計算が確率では重要となりますが、実際に文章問題になるとどれを使うのか悩みますよね。
そんな方は以下の使い分けを読めば10秒で理解できますよ。
いつ使う?確率の計算「PとCと!」の使い分け


確率の文章問題が出てきたら、以下のように使い分けてみましょう。
- !→並べるだけ
- C → 選ぶだけ
- P → 選んで並べる
!を使うときの問題
問 それぞれA,B,C,D,Eと書かれた5枚のカードを一列に並べるとき、並べ方は何通りあるか。


この場合には、並べるだけで「5枚のカードから何枚か選ぶ」といった作業はありません。
このように、ただ一列並べるだけの問題には!(階乗)を使います。
$$5!=5×4×3×2×1=120$$
答え 120通り
よくある問題としては、カードの並べ替えや人を一列に並べる問題です。
Cを使うときの問題
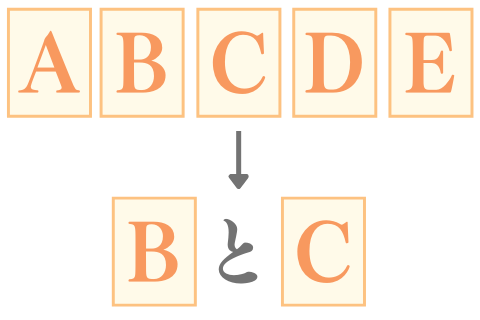
問 それぞれA,B,C,D,Eと書かれた5枚のカードからランダムで2枚を選ぶ。このとき、何通りの選び方があるか。
この問題のように、ただ「選ぶだけ」のときにはCの登場です。

$${_5C_2}=\dfrac{5!}{2!(5-2)!}=10$$
答え 10通り
Pを使うときの問題
問 それぞれA,B,C,D,Eと書かれた5枚のカードから3枚のカードを選んで1列に並べるとき、並べ方は何通りあるか。
こういった問題では、まず「5枚から3枚選ぶ」という行動があります。
さらに、選んだ3枚を「1列に並べ替える」という行動があります。
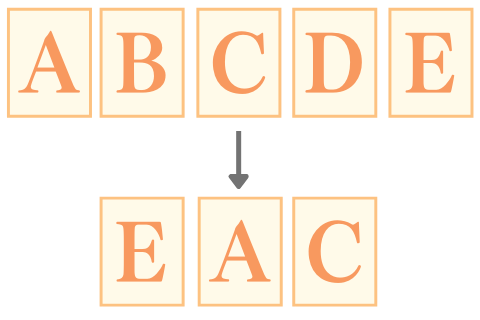

このように、「選んで並べる」ときにはPを使いますよ。
$${_5P_3}=\dfrac{5!}{(5-3)!}=60$$
答え 60通り
PとCと!の使い分けは案外カンタン
教員時代には、「PとCの違いがわからない」「PとCどっちを使えば良いかわからない」といった質問が多く寄せられました。
しかし、こうして整理をしてみると、PとCの違いは明らかですし、使い分けも案外カンタンです。
- 「!」→並べるだけ
- 「C」 → 選ぶだけ
- 「P」→ 選んで並べる
文章題は、どういった作業が必要なのか、それを計算(式)に変換するとどうなるのかといったことを考える必要があります。
そのため、「いつどの式を使えば良いのかを頭の中で整理しておくこと」が数学を得意になる近道となります。
今回のように自分で疑問を持ったときは、一度ノートなどに使い道をまとめてみると良いでしょう。
定期テストで点数を伸ばしたい人、大学受験に失敗したくない人は、高校在学中の3年間は計画的な勉強を日々おこなう必要があります。
自習で理解しきれない、やる気が続かないといった人は学習塾や教材をうまく活用することも今一度検討してみてくださいね。
\ 今すぐチェック! /
おすすめ記事はこちら


関連記事をチェック!
数学に関する以下の関連記事もぜひチェックしてみてくださいね。

