【魔法の言葉で理解】必要条件と十分条件のイメージやコツまとめ

必要条件と十分条件の定義がよくわからない、矢印の向きがどっちかわからなくなる。

そんな声にお応えして、今回は必要条件と十分条件のイメージイラストを使いながら解き方のコツをわかりやすく解説します。

＼　今すぐチェック！　／

「必要条件」「十分条件」の定義をわかりやすく解説

まずは、

の定義を確認しておきましょう。

必要条件と十分条件の定義

必要条件と十分条件の定義は、以下の通りです。

これだけ見ても、ほとんどの人は「何言ってるの？」という感じではないでしょうか。

正直私も学生時代は、この定義を読んでもまったくピンとこずに「？？？」という感じでした。

定義をわかりやすく解説

定義だけ読んでもピンと来ない人は、この定義をもっとかみ砕いた説明を読んで内容を理解する必要があります。

この定義がわかりにくくなっているのは、主語が変わってしまうから。

「qは」と「pは」という違った見方が必要になるから分かりづらいのです。

そのため、「p」を主語と考えpの立ち位置を変えずに見るのがポイント。

この定義を言い換えると、

ということなのです。

しかし、これでもちょっと何言ってるかわからない……

という人も多いかと思います。

そこで、とりあえずテストで出る問題を実践的に取り組んでみましょう。

「必要条件」「十分条件」「必要十分条件」の判定問題を解いてみよう！

定義の解説を見ていても、やっぱりピンとこない人もいるでしょう。

そこで、実践的に問題に取り組んでみることも大切です。

問題が解けるようになると、なんとなく定義も理解できるようになります。

「必要条件」や「十分条件」は以下のような問題として出題されることがほとんどです。

問題

文字はすべて実数とする。次の□に当てはまるものを，(ア)～(エ)から選べ。

問1　$x=2はx^2-5x+6=0であるための□$

とりあえず、これを解いてみましょう。

解答・解説

条件の見分け方は、とりあえず$p⇒q$の形に直すのがポイント。

実際に問題を解く際には、真偽を丸バツでメモする感じにすると、時短になります。

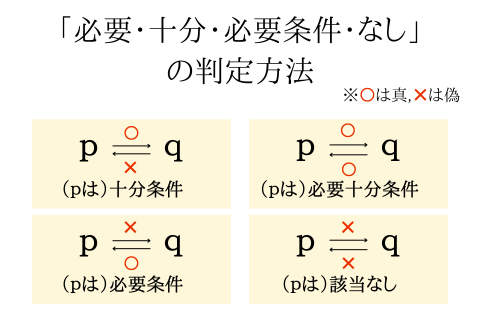
実際の問題には「p」や「q」がそのまま出てくるわけではないので、問題文に出てきた文章や式に置き換えて考えます。

$x=2はx^2-5x+6=0であるための□$の場合、

の2つについて考えます。

① $x=2ならばx^2-5x+6=0$は成り立つのか。

これは、実際に$x=2$を$x^2-5x+6=0$の式に代入してみれば良いですよね。

代入すると、左辺は$2^2-5×2+6$となり、計算すると0になります。

よって、成り立っているので①は真（○）ですね。

次に②を考えます。

ここでまず考えるべきは、$x^2-5x+6=0$について。

これを因数分解してみましょう。

すると、$(x-2)(x-3)=0$となり、解は$x＝2,3$です。

つまり、文章を言い換えると② $x=2,3ならばx=2$となります。

わけて考えてみましょう。

$x=2ならばx=2$は成り立ちますが、 $x=3ならばx=2$は成り立ちません。

反例をあげるなら$x=3$。

よって、成り立たないので②は偽（×）ですね。

つまり、この問題の答えは「十分条件」なので(ウ)になります。

必要条件・十分条件を解くコツ「魔法の言葉」を伝授！

必要条件か、十分条件か、必要十分条件かを解く問題。

なんだか日本語が難しくて解きにくい、というパターンも結構あります。

そこでここでは、魔法の言葉を使って問題を解くコツを伝授いたします。

⇒を「ならば絶対に」か「は絶対に」
という言葉に置き換えてみる

例えば

は真か偽かという問題があるとします。

⇒は「ならば」と言い換えるべきなのですが、

と言い換えてもちょっとわかりづらいです。

そこで今度は「ならば絶対に」「は絶対に」という言葉に置き換えてみましょう。

今回は「は絶対に」の方が日本語的にわかりやすいですね。

「うさぎは絶対に動物」は明らかに○

「動物は絶対にうさぎ」は動物というのはうさぎに限った話ではないため、（犬や猫も動物）×だとわかります。

このように、「⇒（ならば）」は

という言葉に置き換えてみると日本語的にわかりやすくなります。

公式的な方法ではありませんが、なんだか日本語の文章としてわかりにくいな、と感じたらこの「魔法の言葉」を使ってみてください。

必要条件と十分条件を一発で覚える！矢印の向きイメージ図

必要条件と十分条件って、矢印の向きがどっちかわからなくなることはありませんか？

私はすぐに忘れます。

矢印の向きは二択ですが、二択だからこそテストになると「こっちの向きで合ってたっけ……」と不安になってくることもあります。

矢印の向きを間違ってしまうと、答えがすべて逆になってしまい、テストでも大変な結果になりかねません。

そこで今回は、矢印の向きがどっちかわからなくなることがないように、2パターンのイメージ図を用意しました。

このイメージをぜひ頭にたたき込んでくださいね。

「じゅうよう」の文字で覚える

十分条件と必要条件の矢印の向きは、「じゅうよう」で覚えるというのが有名です。

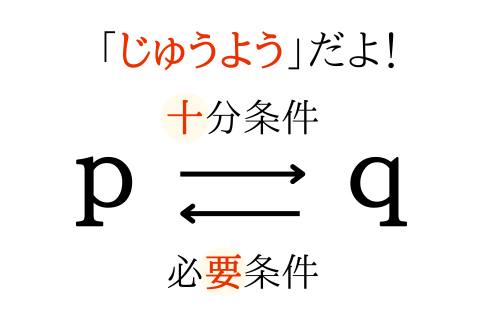
漢字はちょっと違いますが、重要「十要（じゅうよう）」という言葉で覚えると間違いが少ないですよ。

例えば高校数学で最も有名な参考書である「チャート式数学I+A」にもこの覚え方が記載されています。

イメージイラストで覚える

さらに暗記を定着させたいなら、イメージイラストを見ておくのもおすすめです。

実際に、私が学生時代に恩師に教わった覚え方がこちらです。

左側の人が”主人公“と考えてください。

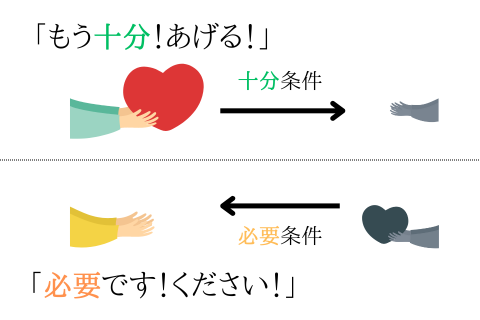
イラストのイメージで覚えると、記憶に残りやすいですよね。

で覚えると良いでしょう。

このイメージを持っておくと、矢印の向きで迷うことがほとんどなくなります。

実際に「あげる・もらう」という動作を身体を動かして表現してみるのもおすすめです。

関連記事をチェック！

数学に関する以下の関連記事もぜひチェックしてみてくださいね。