確率で円順列の公式を学習すると「なぜ1を引くの?」という疑問を持つ人は多いことでしょう。
そこで今回は、円順列の公式でなぜ1を引く必要があるのか、順列と円順列の見分け方や計算方法をわかりやすく解説していきます。
\ 今すぐチェック! /
のキャンペーン
確率の「順列」と「円順列」の計算方法


そもそも定義を知らなければ話しは進みません。
まずは本題に入る前に、順列と円順列の意味を再確認しておきましょう。
順列の定義
いくつかのものを順に1列に並べるとき、その並びの1つ1つを順列という。
異なるn個のものから異なるr個を取り出して並べる順列をn個からr個取る順列といい、その総数を$${_nP_r}$$で表す。ただし、$$r≦n$$である。
定義を見ても正直ピンと来ない人もいるでしょう。
そんな人は、とりあえず計算方法と使い道を確認できればOKです。
順列の計算方法
順列は、以下のように計算をするのがきまりです。
$${_nP_r}=\dfrac{n!}{(n-r)!}$$
具体的な計算方法は、以下の通りです。
$${_6P_4}=\dfrac{6!}{(6-4)!}=360$$
また、$$r=n$$のときは$$n!$$と表し、これを「nの階乗(かいじょう)」と呼びます。
順列はどんな時に使う?
順列は、以下のような文章問題が例として挙げられます。
問 それぞれA,B,C,D,Eと書かれた5枚のカードから3枚のカードを選んで1列に並べるとき、並べ方は何通りあるか。
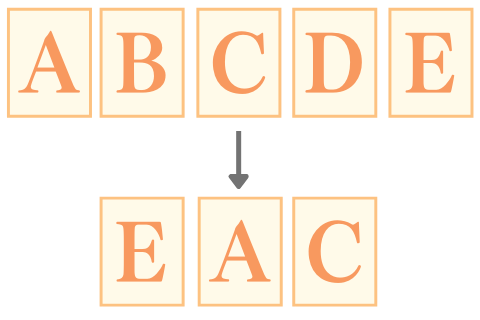

$${_5P_3}=\dfrac{5!}{(5-3)!}=60$$
答え 60通り
円順列の定義
次に、円順列の定義を見てみましょう。
いくつかのものを円形に並べる順列を円順列といい、異なるn個のものの円順列の総数は$$\dfrac{_nP_n}{n}=(n-1)!$$
ここで出てくる(n-1)に疑問を持つ方が多いのではないでしょうか?
なぜ1を引くことになるのか
なぜ1を引くのか、これは後ほどイラスト付きでわかりやすく解説していきます。
円順列の計算方法
円順列の具体的な計算方法は、以下の通りです。
$$\dfrac{_5P_5}{5}=(5-1)!=4!=24$$
円順列はどんな時に使う?
円順列は、以下のような文章問題が例として挙げられます。
問 それぞれA,B,C,D,Eと書かれた5枚のカードを机の上で円形に並べる方法は何通りあるか。
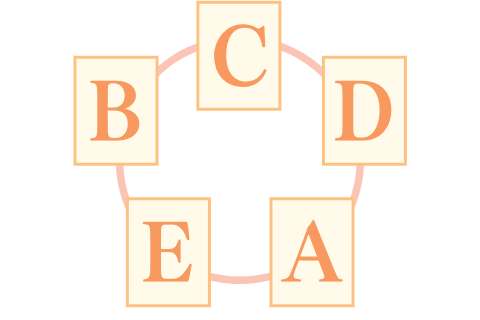

$$(5-1)!=4!=24$$
答え 24通り
さて、いよいよ本題です。
この問題を例に挙げて、円順列の公式ではなぜ1を引くことになるのかを解説していきます。
円順列の公式はなぜ1を引く?


円順列でなぜ1を引くことになるのか。
これは単に「公式だから!」ということではなく、実はちゃんとした意味があります。
1を引くことには
ちゃんとした意味がある
そもそも円順列を考えるときには、順列になかった問題が発生します。
実はこの「1を引く」ということは、その問題を解決するのに大いに役立っているのです。
結論から言うと、
円順列の計算をする際に
1つ固定して他を1列に並べるから
「固定した数の分」で1を引いている
ということです。
これだけ読んでも正直よくわかりませんよね。
以下、イラスト付きで解説していきます。
順列にはなかった円順列の問題点
順列になかったけど円順列になって困ることとはなんでしょうか。
それはズバリ「回転した際に同じ組み合わせが出てきてしまう」という点です。
円順列は回転することによって
生じる問題がある
順列では1列に並べます。
そのため、並べ替えるのは割と簡単ですね。
しかし円順列では、円になっているせいで単に1列に並べるだけだと「重複」してしまう組み合わせが出てくるのです。
円順列で重複しているパターンとは
まずは順列のパターンから。
以下の2つ、はまったく別ものであることがわかります。
2通りとしてカウントOK!


1列に並べるとこれは2パターンですよね。
それでは、これが円順列になった場合のイラストを見てみましょう。




この2つのイラストは2通りとしてカウントしても良いでしょうか?
答えは……いいえ。
この2つのイラストは、同じものと扱われ1通りとしてカウントされます。
それはなぜか。
1通りとしてカウント




左のイラストを右に1文字分、回転させてみてください。
すると、不思議。
右のイラストとまったく同じになることがわかります。
円順列では、このような場合、組み合わせは1つしてカウントすることになっています。
円順列では
「適当に回転して並び方が一致するものは同じ順列」
と考える
理解しにくい場合は「隣は誰か?」という点に着目をしてみましょう。
つまり、右のイラストも左のイラストも以下のようになっていることがわかります。




- Cから見て左はD
- Dから見て左はA
- Aから見て左はE
- Eから見て左はB
- Bから見て左はC
つまり、
- 左のイラスト:「C→D→A→E→B」
- 右のイラスト:「B→C→D→A→E」
となんだか違うものに見えてしまいますが、回転させると実態は同じであるということです。
左のイラスト:「C→D→A→E→B」を右に1個分ズラすと……
「B→C→D→A→E」になる
このように、円順列でやっかいなのは「回転した際に同じ組み合わせが出てきてしまう」ということです。
つまり単純に、1列に並べるということではダメなんですね。
そこで登場するのが「1枚を固定しよう!」という考え方です。
円順列で1を引くのは1枚を固定して計算するから
円順列を公式化する際に、人はどうするか考えます。
回転すると、同じ組み合わせが違ったものに見えてしまう……
計算しにくい……
じゃあ「回転しなくなれば良い」よね
というまさかの発想です。
回転を止めて計算をしやすくするためには、1枚を固定すればOK。
例を見てみましょう。
先ほどのパターンで、Cをこの位置で固定するとします。
Cはこの位置で固定!動かしません


そうすると、「A」「B」「D」「E」は自由に動いてOK。
Cが固定されれば回転する分を考えなくて良いため、単純に「A」「B」「D」「E」を1列に並べるという計算で済むのです。
つまり、
問 それぞれA,B,C,D,Eと書かれた5枚のカードを机の上で円形に並べる方法は何通りあるか。
の問題は、C以外の4枚を1列に並べる計算で求められることになります。
$$(5-1)!=4!=24$$
答え 24通り
ちなみに、Cじゃなくて固定するのはAでもBでも何でもOK。
とにかく「1枚を固定する」という考えが重要です。
1枚を固定することで「他を1列に並べることで計算が完了する」ということが肝となるのです。
つまり、円順列の公式でなぜ1を引くのかと言うと以下のまとめになります。
円順列の計算をする際に
1つ固定して他を1列に並べるから
「固定した数の分」で1を引いている
「普通の順列」と「円順列」の見分け方


さて、文章問題が出てきたときに「これは普通の順列問題?」「円順列の問題?」と疑問に思うこともあるでしょう。
そこで順列と円順列の問題のカンタンな見分け方について解説していきます。
円順列の公式を使って計算する問題
順列の問題は星の数ほどパターンがあるため、円順列の公式を使って求める文章問題のパターンを頭に入れておくのがポイントです。
文章問題で、以下のような文言があれば円順列といってほぼ間違いないでしょう。
- ○人の生徒は丸いテーブルに座る
- ○人が手をつないで輪を作る
- ○を円周上に並べる
こういった文言がなければ、普通の順列や他のパターンを考える必要が出てきます。
円順列っぽいのに円順列の公式が使えない問題
以下のような文言がある文章問題では、円順列の公式をそのまま使うことができません。
- 首輪
- 数珠
- ブレスレット
- 玉には中心を取って穴が空いている
- 玉にひもを通し輪を作る
これらはいわゆる「じゅず順列」と呼ばれる公式を使います。
つまり、円の形になっていても裏返せるもの「数珠・ブレスレット・首輪」といったキーワードが出てくるものは「円順列の公式を使って解く問題ではない」ということを覚えておきましょう。
現実的に考えて
「裏返せるもの」はじゅず順列
じゅず順列については、また別の記事にて解説したいと思います。
関連記事をチェック!
数学に関する以下の関連記事もぜひチェックしてみてくださいね。

