高校で習う難しい因数分解を解くコツについてまとめました。
そもそも中学の因数分解より高校の因数分解が難しく感じるのはなぜか、因数分解が苦手になる本当の理由なども解説していきます。
\ 今すぐチェック! /
のキャンペーン
高校の難しい因数分解も実はパターンが決まっている


数学Ⅰで学習する因数分解が「苦手」「難しい」と思う人は実は結構多いと思います。
しかし、これは割とごく自然なことで悲観する必要はありません。
高校で習う因数分解は、中学校で習った因数分解とは比較にならないほど難しくなるからです。
中学より高校の因数分解の方がパターンが多い
例えば、中学校で習う因数分解の公式は以下の5つでしたね。
① $ ab+ac=a(b+c) $
② $ x^2+(a+b)x+ab=(x+a)(x+b)$
③ $x^2+2ax+a^2=(x+a)^2$
④ $x^2-2ax+a^2=(x-a)^2$
⑤ $x^2-a^2=(x+a)(x-a)$
例えば①の公式なら、以下のような時に使えました。
例:$4ab−12b=4b(a−3)$
上記は共通因数である $4 b$ をくくり出した形です。
つまり、中学の因数分解はこの5つを活用すれば必ず解ける問題になっているわけです。
そのため5パターンの解き方がわかれば良いので「中学校のときは因数分解ができた」という人が多いのです。
高校で習う因数分解もパターンは決まっている
中学数学と同様に、実は数学Ⅰで学習する因数分解もどんなに難しいものでもパターンが決まっています。
中学で習う「くくり出し」ような公式で表しきれないものもありますが、解き方自体のパターンは決まっているのです。
つまり、そのパターンさえマスターしてしまえば、数学Ⅰで習う範囲の因数分解であれば解けない問題は出てこないのです。
因数分解が難しいと感じてしまう本当の理由
以上の事実から、因数分解ができないからといって
「自分は頭が悪い」
「数学のセンスがない」
といったことを感じる必要はありません。
なぜならば、高校の因数分解が難しいと感じてしまう本当の理由は、ただ因数分解のパターンを知らないだけだからです。
解き方を知らない問題は、いくら考えても解くことはできません。
例えば足し算を習ったばかりの小学1年生に、いきなり割り算の問題を出しても普通解けませんよね?
因数分解もそれと同じです。
そもそもやり方を知らないと、問題なんて解けるわけないのです。
高校の因数分解は誰でも解けるようになる
高校数学ともなると、頭を抱えたくなる問題は多いのですよね。
しかしそんな中でも、因数分解に関しては正直パターンさえマスターすれば誰でも解けるようになります。
1日で解決する!難しい因数分解を解くコツは?


この記事を読んでいるということは、難しい因数分解に悩んでいる方も多いのではないでしょうか。
先ほど解説した通り、難しい因数分解を解くコツはズバリ、パターンを覚えることです。
難しい因数分解を解くコツは
パターンを覚えること
よく「数学は暗記教科ではない」という人もいますが、公式や解き方に関してはちゃんと覚えないと問題は解けません。
そのため、因数分解もパターンを覚える必要があります。
難しい因数分解のパターンは何個ある?
先ほど中学数学で習う因数分解は5パターンだという話をしました。
では、数学Ⅰで習う因数分解のパターンはいくつあるのでしょうか。
おおよそのパターンを書き出すと以下の通りになります。
- たすき掛け
- 置き換え
- 最低次の文字について整理
- 平方の差を作る
- 2元2字式
- 1つの文字について整理
つまり、中学で習った5パターンにさらに6つ程度のパターンが追加されるということです。
そのため、パターンを把握しきれずに因数分解が苦手になってしまう人が多いのです。
ちなみに置き換えを利用する因数分解は以下の記事で解説して見ました。


本気でやれば1日!チャート式なら10ページで解決
パターン自体は多くないですが、例題を示そうとするととてもここでは書き切れないためおすすめの参考書を紹介しておきます。
高校数学を攻略するなら、とにかく解法を習得することが鍵となります。
そのため、こうしたパターンを勉強するなら「チャート式」シリーズが最もおすすめです。
チャート式は、パターン1つ1つに対してページごとに理解しやすい構造になっています。
1ページ1テーマで演習できるようになっている優秀な参考書です。
そのため、因数分解のパターンを1つずつ確実に習得するのに向いていますよ。
チャート式だと、だいたい因数分解の演習ページは10ページ程度。
(コラムや公式まとめ、エクササイズページなどを除いた場合)
つまり、たった10ページ問題集を解くだけで難しい因数分解でも確実に解けるようになります。
このページ数であれば、休みの日に丸一日本気を出してやるだけで因数分解のパターンを攻略できる人も多いでしょう。
ちなみに、チャート式のような問題集を使って自分で勉強をすすめるのが苦手という人は、動画授業を活用するのがおすすめです。
会員数は157万人!
\ 2週間無料でおためし /
進研ゼミでも有名なベネッセが提供している「スタディサプリ」なら2週間の無料期間があります。
2週間以内に解約すれば、費用は一切かかりません。
そのため、「今分からなくて困っている分野の動画だけ試しに見てみる」というのでも良いでしょう。
悩みが解決できそうであれば、継続して利用するのもおすすめです。
難しい因数分解を解く5つのステップ
チャート式を使って演習をすれば、因数分解のパターンを理解しやり方を覚えることができます。
そのため、難しい因数分解の問題が出ても「どのパターンで解くのか?」ということだけわかれば解けるようになるんですね。
ちなみに、パターンを取得した後は以下の5ステップで難しい因数分解にアタックしてみてください。
難しい因数分解を解く5つのステップ
(公式が使えない問題は3へ)
この5ステップで、基本的に難しい因数分解の問題も解けるはずです。
因数分解の問題は共通テストでもそのまま出る!


因数分解というと、高校数学Ⅰで習う”基本的な知識”と考える人も多いでしょう。
しかし、因数分解は侮れません。
因数分解は、今後高校数学を習う際にとても重要となるだけでなく、直接的に「共通テスト」で出題されるからです。
共通テストで
因数分解の問題が出る
その証拠に、2021年の共通テストでは「第1問」に因数分解の問題が出題されています。
実際に出題された例を見てみましょう。
2021年の共通テスト【数学Ⅰ・A】
第1問
[1]$cを正の整数とする。xの2字方程式$
${2x^2+(4c-3)x+2c^2-c-11=0}……①$
$について考える。$
(1) $c=1のとき,①の左辺を因数分解すると$
$(アx+イ)(x-ウ) であるから,$
$①の解は x=-\dfrac{イ}{ア},ウ である。$
まず $c=1$ を代入し、因数分解をするだけの問題です。
これを先ほどのステップに照らし合わせて解いてみましょう。
5つのステップをもう一度確認
(公式が使えない問題は3へ)
$c=1を代入すると、$
${2x^2+x+-10=0}となります。$
$この場合、5つのステップのうち、$
[STEP1] 共通因数がくくり出せないためSTEP2へ進む
[STEP2] 公式が使えるかを確認。
この問題の場合、2元3項式で「たすき掛け」が使えます。
つまり、たすき掛けを利用して解決ができるためここで終わりです。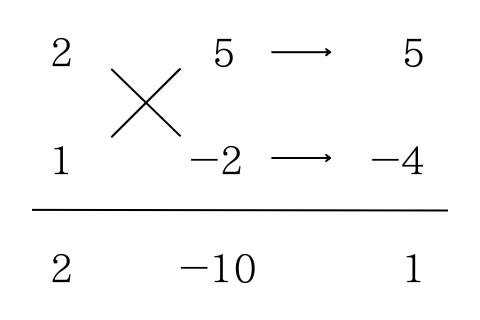
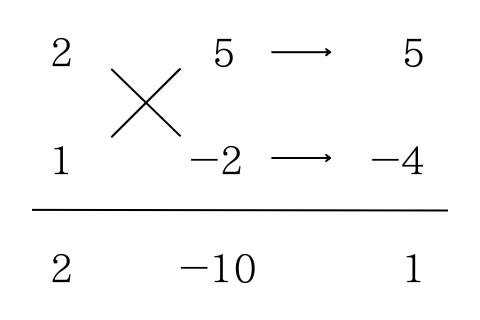
${(2x+5)(x-2)=0}となります。$
$よって解は、x=-\dfrac{5}{2} , 2$
この問題が解けるだけで、共通テストの数学Ⅰ・Aで2点をゲットできます!
そう思うと、なんだか希望がもてる気がしませんか。
因数分解は共通テストも重要視されている
このように、因数分解は共通テストでも重要視されていることがわかります。
因数分解ができれば共通テストでも確実に点数をゲットできますね!
そのため、因数分解は計算ミスも0になるくらい、高校1年生のうちにしっかり習得しておくことが大切です。
因数分解をマスターしておけば、その後の学習もグッと楽になりますよ。
関連記事をチェック!
数学に関する以下の関連記事もぜひチェックしてみてくださいね。


